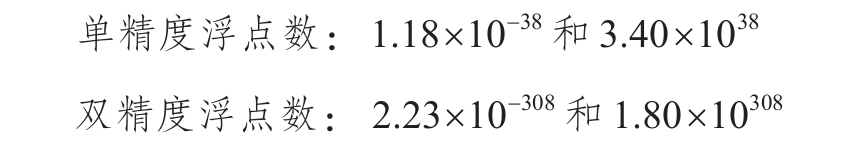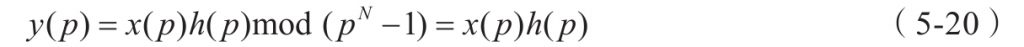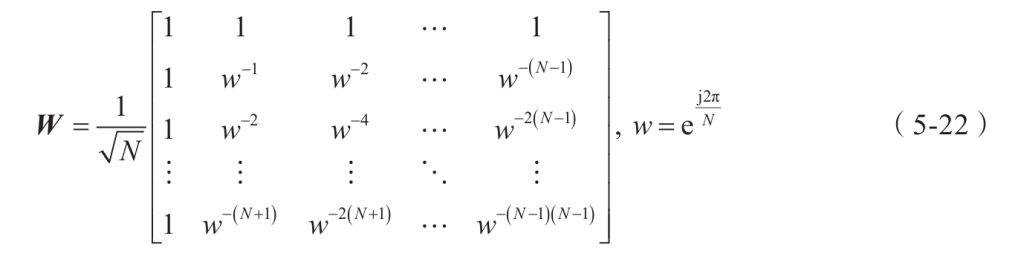简答题 4分×8个=32分
分析题 7分×4个=28分
设计题 40分 (1000~1200字)用什么算法,讲清楚
第1章 绪论
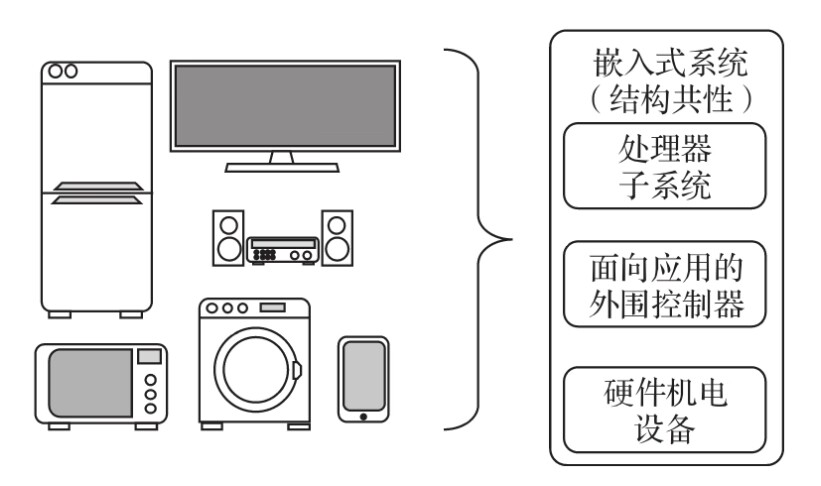
嵌入式系统(结构共性)
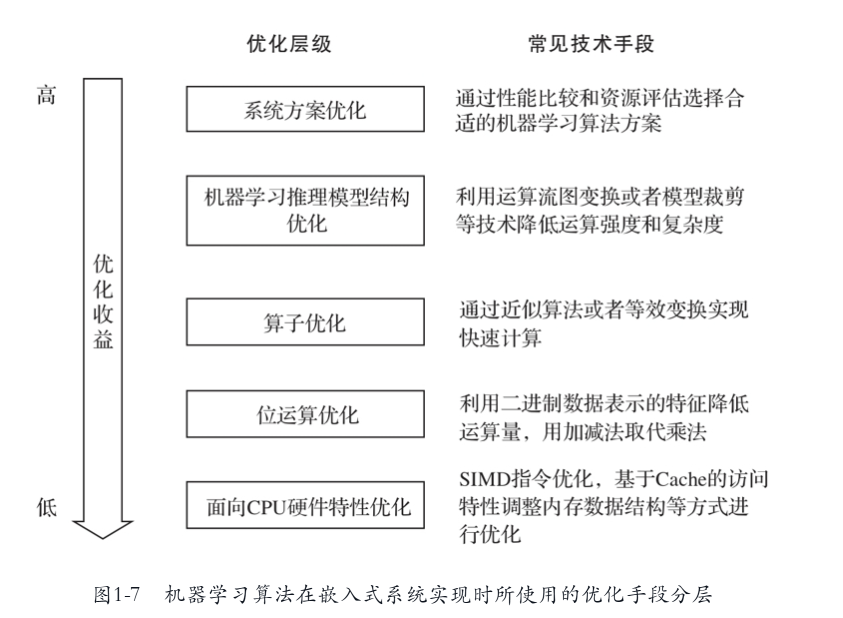
机器学习算法在嵌入式系统实现时所用的优化手段分层 (会画图,内容会描述)
第2章 嵌入式软件编程模式和优化
常见的嵌入式系统运行模式 P9-17
2.2通用软件优化方法 P20
第3章 机器学习算法概述
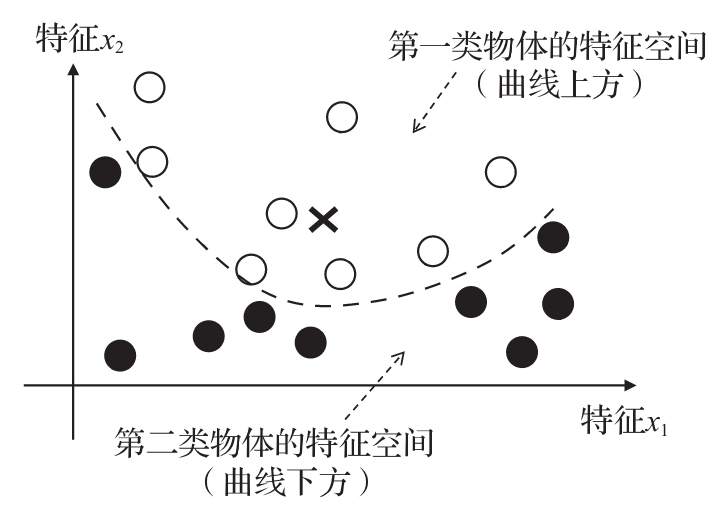
3.3 SVM分类器 (知道怎么回事)P40
3.6 神经网络
3.6.1 原理概述
2.卷积运算 (画图或会写伪代码)
神经网络中的卷积运算主要是二维卷积,它可以看成滑动窗口在需要卷积的特征数据上移动,在每个移动位置计算窗口内元素的加权和,如图3-10所示。
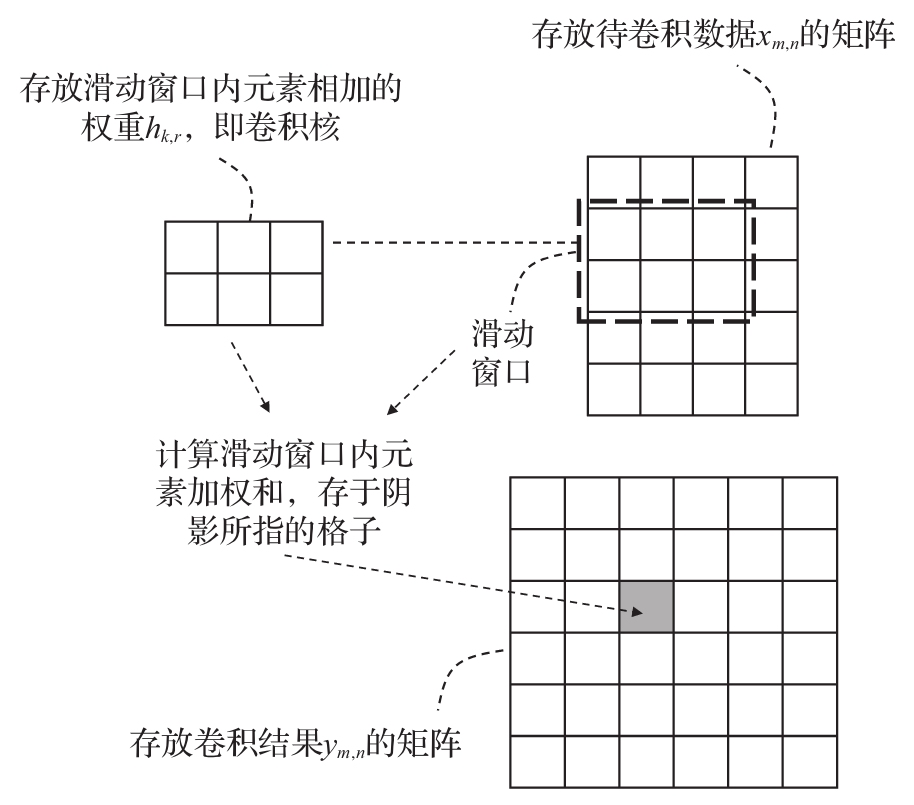

在很多神经网络软件框架中,卷积运算被转换成矩阵乘法实现,下面通过一个简单的例子说明。图3-11给出了一个二维卷积的例子。
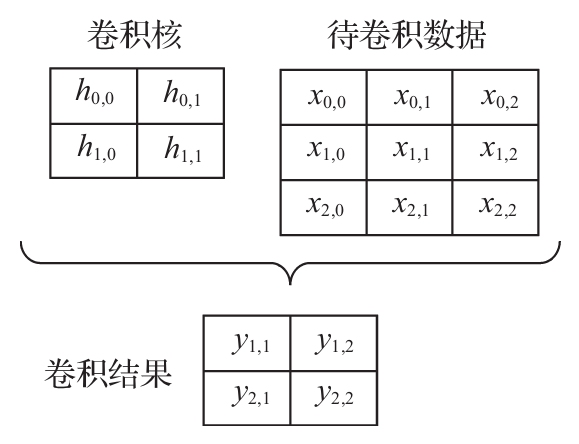
图3-11中给出的4个卷积结果对应的运算为
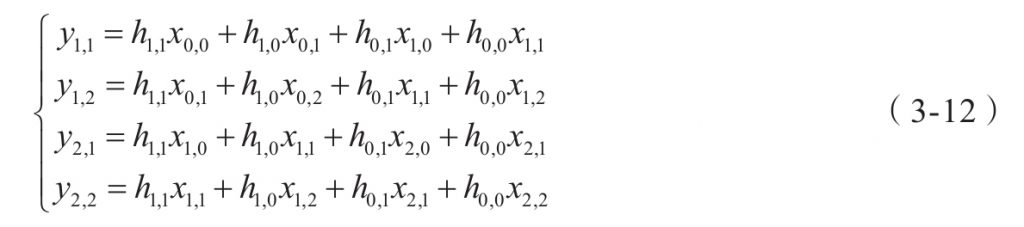
上面的运算是线性运算,可以写成下面的矩阵形式:
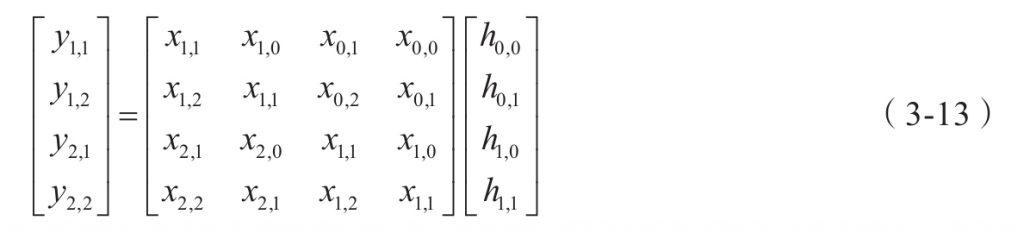
伪代码 P209
3.6.2 模型训练和推理
神经网络结构(一定会画LeNet结构)P51
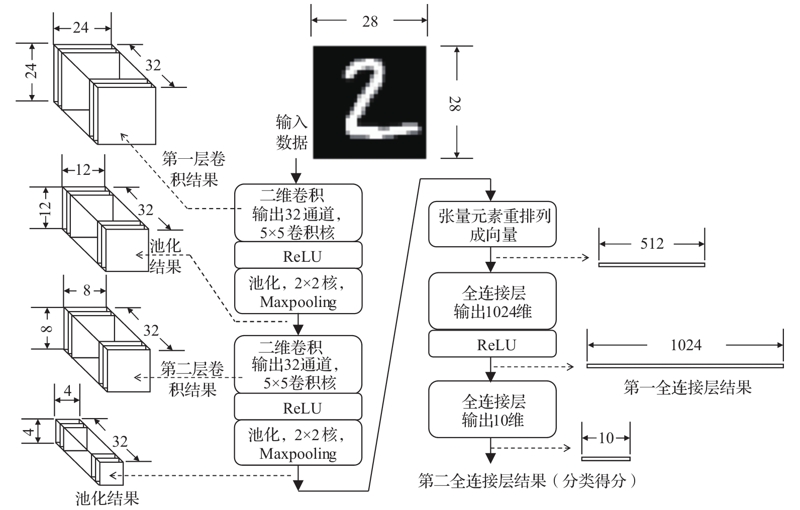
神经网络运算流程的描述如下:
1)第一个卷积层使用32个5×5的卷积核对28×28原始图片进行卷积,得到32个24×24的卷积结果,经过ReLU激活函数运算并池化后,得到32个12×12的特征图。
2)第二个卷积层使用32个32通道的5×5卷积核,作用于上一层数据得到32个8×8的特征图,经过ReLU和池化后得到32个4×4特征图。
3)第二卷积层处理结果被“拉直”成512维(512=32×4×4)的向量。
4)第一个全连接层,该层输出1024维的向量,输出同样经过ReLU函数运算。
5)第二个全连接层,该层输出10维向量,作为10个数字类型的匹配“得分”。其中“得分”最高的元素对应于原始图像对应的最可能的数字。
上述神经网络通过现成的神经网络框架能够高效地构建和训练。代码清单3-6所示是基于Pytorch的神经网络构建的代码。
第4章 数值的表示和运算
4.1 浮点数
4.1.1 单精度和双精度浮点数
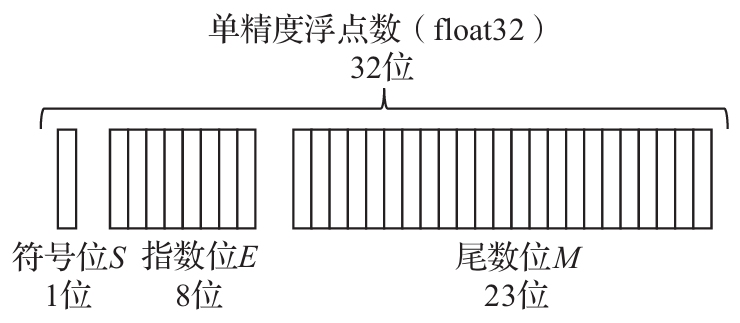
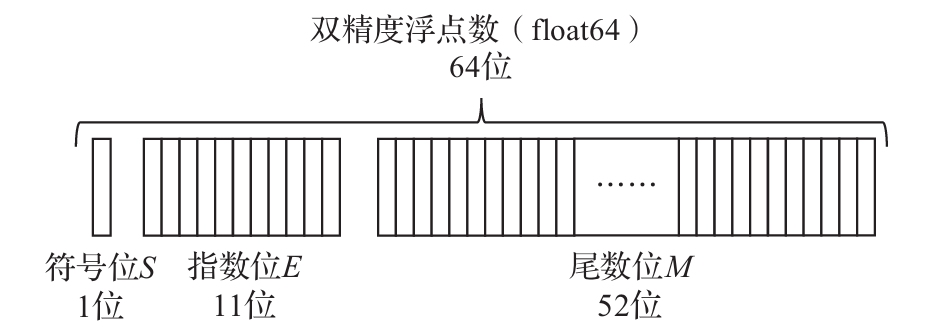
存储的内容包括三部分:符号位S、指数位E和尾数位M。其中指数位E存储指数值的二进制编码,对于单精度浮点数,其对应指数值是,对于双精度浮点数,对应指数位为。尾数位M有两种格式——规范化格式和非规范化格式。这里主要讨论规范化格式,在这一格式下,M用于记录形如(1.xxxx)2的二进制数,小数点的左边固定为1,因此M中不需要额外保存这个1,只保存小数点之后的内容。对于规范化的普通浮点数,单精度数中E的取值范围是1~254,双精度数中E的取值范围是1~2046。从以上特点可以看到,对于规范化表示形式,浮点数的具体值如下。
- 单精度浮点数数值(规范化):

- 双精度浮点数数值(规范化):

这个127和1023是什么东西?答:是偏置。为什么要有偏置?答:使指数以无符号形式存储,便于浮点数加减运算时候对阶操作。为什么是127和1023?答:E全0时,根据S为0或1表示+0和-0,;E全1时,根据M全0或非全0表示无穷或无效数。[0,255]变成[1,254],[1,254] -127 得到 [-126,127]
下面给出一个具体的32位单精度浮点数的例子:
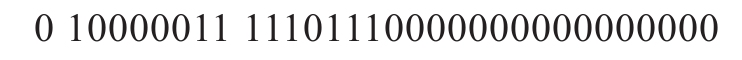
如上所示的32位数据对应:
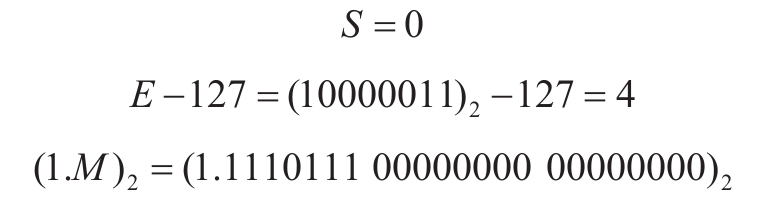
于是,它对应的数值是
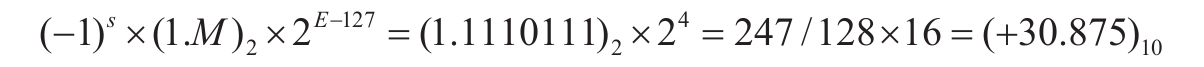
下面是双精度浮点数的例子,对应的数据是![]() 。它在双精度浮点数格式中显示为
。它在双精度浮点数格式中显示为
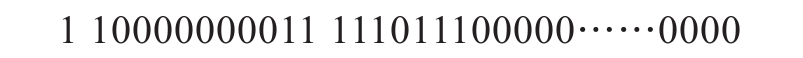
如上所示的64位数据对应:
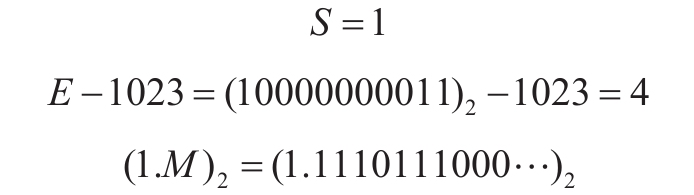
它所表示的数值为
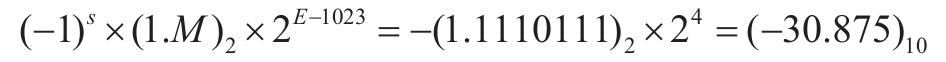
4.3仿射映射量化
4.3.2 量化数据运算(乘法解释)P83-84
仿射映射变换使用下面的公式将量化符号q和它表示的实数d对应起来:

其中d是实数,q是整数,是实数d的量化表示,z是零点,代表实数0的量化表示,通常也用整数表示,s是量化步长,代表上述量化数能够表示的两个实数数值的最小间隔。对于任意给定的实数d,仿射映射量化过程就是根据(s,z)计算它的量化符号q,使得s(q-z)和d最接近,具体算法如下:

下面我们讨论使用仿射映射量化的数据的运算。讨论过程中使用记号(s,z,q)表示为量化中心为z、步长为s以及量化符号为q的仿射映射量化数据。考虑两个量化数

根据乘积关系c=ab可以得出
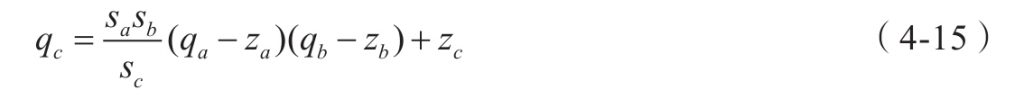
其中![]() 使用整数乘法即可完成,不需要进行浮点运算。对于
使用整数乘法即可完成,不需要进行浮点运算。对于![]() 的计算,通常需要用到浮点数运算,但我们可以使用整数乘法加上移位实现。这通过下面的例子说明。比如
的计算,通常需要用到浮点数运算,但我们可以使用整数乘法加上移位实现。这通过下面的例子说明。比如![]() ,我们希望计算它和整数x的乘积,首先可以将0.7近似表示为下面的形式:
,我们希望计算它和整数x的乘积,首先可以将0.7近似表示为下面的形式:
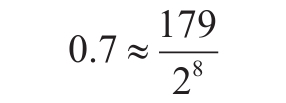
于是
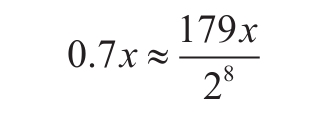
其中分子计算只需要进行整数乘法,而分母对应的除法只需要移位操作实现。类似算法的更多细节可以在4.4节找到。
第5章 卷积运算优化
5.2 快速卷积算法
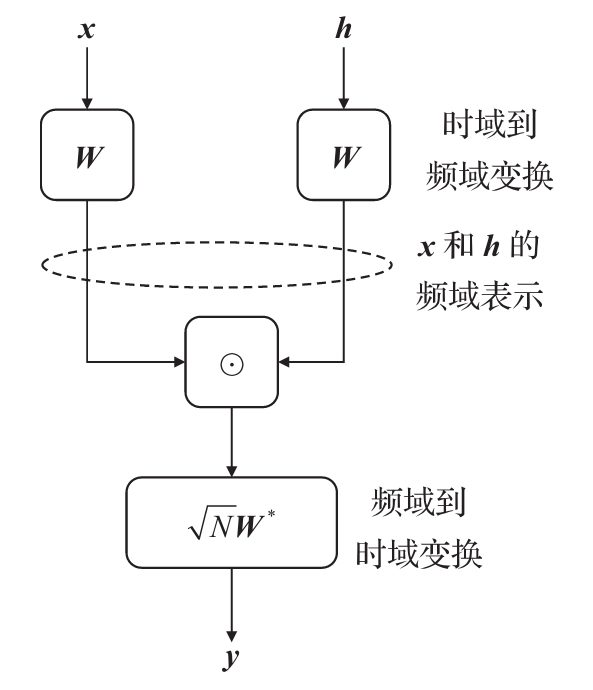
5.2.1 一维循环卷积频域快速算法 (理解卷积怎么到频域)P114~
两个长度同为N的序列 x、h,分别进行离散傅里叶变换,相乘,再进行离散傅里叶反变换,得到x与h循环卷积的结果。
*卷积定理:卷积定理是傅立叶变换满足的一个重要性质。卷积定理指出,函数卷积的傅立叶变换是函数傅立叶变换的乘积。具体分为时域卷积定理和频域卷积定理,时域卷积定理即时域内的卷积对应频域内的乘积;频域卷积定理即频域内的卷积对应时域内的乘积,两者具有对偶关系。
5.3 近似卷积算法 (几种近似卷计算法)
第8章 ARM平台上的机器学习编程
嵌入式处理器分类
FPGA:现场可编程逻辑门阵列
FPGA 器件属于专用集成电路中的一种半定制电路,是可编程的逻辑列阵,能够有效的解决原有的器件门电路数较少的问题。FPGA 的基本结构包括可编程输入输出单元,可配置逻辑块,数字时钟管理模块,嵌入式块RAM,布线资源,内嵌专用硬核,底层内嵌功能单元。由于FPGA具有布线资源丰富,可重复编程和集成度高,投资较低的特点,在数字电路设计领域得到了广泛的应用。FPGA的设计流程包括算法设计、代码仿真以及设计、板机调试,设计者以及实际需求建立算法架构,利用EDA建立设计方案或HD编写设计代码,通过代码仿真保证设计方案符合实际要求,最后进行板级调试,利用配置电路将相关文件下载至FPGA芯片中,验证实际运行效果。
MPU:嵌入式微处理器
嵌入式微处理器是由通用计算机中的CPU演变而来的。它的特征是具有32位以上的处理器,具有较高的性能,当然其价格也相应较高。但与计算机处理器不同的是,在实际嵌入式应用中,只保留和嵌入式应用紧密相关的功能硬件,去除其他的冗余功能部分,这样就以最低的功耗和资源实现嵌入式应用的特殊要求
MPU是计算机的计算、判断或控制中心,有人称它为”计算机的心脏”。
MCU:嵌入式微控制器
微控制单元(Microcontroller Unit) ,又称单片微型计算机(Single Chip Microcomputer )或者单片机。
是把中央处理器的频率与规格做适当缩减,并将内存(memory)、计数器(Timer)、USB、A/D转换、UART、PLC、DMA等周边接口,甚至LCD驱动电路都整合在单一芯片上,形成芯片级的计算机,为不同的应用场合做不同组合控制。诸如手机、PC外围、遥控器,至汽车电子、工业上的步进马达、机器手臂的控制等,都可见到MCU的身影。
DSP:嵌入式DSP处理器
嵌入式DSP处理器(Embedded Digital Signal Processor,EDSP)是一种非常擅长于高速实现各种数字信号处理运算(如数字滤波、频谱分析等)的嵌入式处理器。由于对DSP硬件结构和指令进行了特殊设计,使其能够高速完成各种数字信号处理算法。
SOC:嵌入式片上系统
SOC的定义多种多样,由于其内涵丰富、应用范围广,很难给出准确定义。一般说来, SOC称为系统级芯片,也有称片上系统,意指它是一个产品,是一个有专用目标的集成电路,其中包含完整系统并有嵌入软件的全部内容。同时它又是一种技术,用以实现从确定系统功能开始,到软/硬件划分,并完成设计的整个过程。
从狭义角度讲,它是信息系统核心的芯片集成,是将系统关键部件集成在一块芯片上;从广义角度讲, SoC是一个微小型系统,如果说中央处理器(CPU)是大脑,那么SoC就是包括大脑、心脏、眼睛和手的系统。国内外学术界一般倾向将SoC定义为将微处理器、模拟IP(Intellectual Property)核、数字IP核和存储器(或片外存储控制接口)集成在单一芯片上,它通常是客户定制的,或是面向特定用途的标准产品。
ARM处理器主要分三个系列:Cortex-A/M/R
Cortex-A
该系列处理器侧重复杂应用,能够运行类似Linux级别的操作系统。在操作系统支持下运行多任务应用程序,提供丰富的人机交互功能。这一类处理器关注运算性能,功耗和速度相对较高,应用领域包括平板电脑和彩屏手机等。
Cortex-M
该系列处理器针对工业控制应用,在外围接口控制器和片内运算加速硬件的选择上根据工业应用需求进行优化,平衡外围电路复杂度、系统功耗、可靠性和成本。Cortex-M系列处理器在片内存储和运算能力上低于Cortex-A系列处理器,但它在工业控制和消费类家电产品中得到广泛应用。在大多数嵌入式应用系统中,Cortex-M处理器往往站在“幕后”,不直接参与用户界面操作,比如用于设备的电源控制、传感器芯片数据传输和接口管理等。
Cortex-R
这一系列处理器面向需要实时,快速响应的应用,对功耗、性能和封装形式进行了优化,使之适用于可靠性和容错要求更高的工业应用领域。
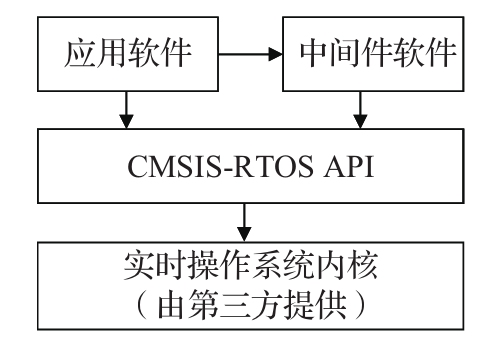
8.1 CMSIS软件框架概述
会分层
CMSIS(Cortex Microcontroller Software Interface Standard)
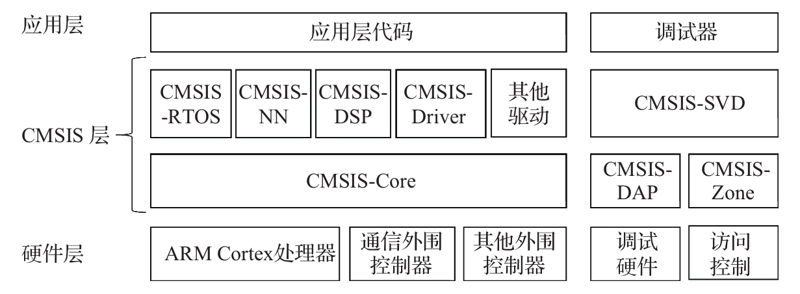
图8-1的左侧列出了CMSIS软件的三个分层:应用层、CMSIS层、硬件层,中间的CMSIS层包括了独立于具体的ARM处理器型号的软件模块,它们规定了和ARM处理器平台无关的通用接口规范。最下层硬件层是和ARM处理器型号以及外围控制器相关的定义。CMSIS框架的核心部分包括了多个子模块,下面简要列出这些子模块的功能说明。
8.5.2 基于ONNX格式的机器学习模型构建
:你要知道onnx这个格式
1.ONNX数据格式概述
ONNX是英文Open Neural Network Exchange的缩写,它是一种开放的神经网络数据格式。不同的神经网络训练框架对应的数据模型可以转换成ONNX格式表示,目前已有的转换工具支持TensorFlow、Caffe,Pytorch,Microsoft Cognitive Toolkit,Apache MXNet等神经网络框架输出的模型数据文件和ONNX数据格式之间的相互转换。
ONNX除了用于描述神经网络模型之外,也能够用于描述其他机器学习算法模型,包括随机森林、SVM等常见的机器学习模型。现有的转换工具支持将Scikit-Learn软件包训练生成的机器学习模型转成ONNX格式。
ONNX文件格式有不同的版本,每个版本支持的神经网络或者机器学习的算子范围各不相同。ARM NN目前支持的ONNX的算子类型有限,一些复杂的ONNX模型数据还不能够直接被ARM NN解析,但ARM NN对ONNX的支持在不断扩展中。目前对ONNX所定义的算子支持比较全面的有微软的ONNX-Runtime,它分为x86和ARM版本,可以从GitHub下载编译得到ONNX的模型数据的执行环境。
通过ONNX格式“中转”可以实现不同神经网络框架生成的网络数据模型格式转换。下面列出部分ONNX格式转换软件包(Python下的软件包):
·sklearn-onnx——将Python下的Scikit-Learn训练得到的机器学习模型转成ONNX格式。
·tensorflow-onnx(tf2onnx)——将TensorFlow模型转成ONNX格式。
·keras2onnx——将Keras模型转成ONNX格式。
·ONNXMLTools——包括多个机器学习或者神经网络框架数据文件转成ONNX的工具,包括Keras、TensorFlow、Scikit-Learn、Apple Core ML、Spark ML、LightGBM、libsvm、XGBoost、H2O。